English (UK) 
Deutsch (Deutschland) 
Computational Fluid Dynamics (CFD)
W
e use CFD simulations to understand, analyze and solve various complex problems that involve fluid flow.
The various parameters (like pressure, temperature, velocity, volume fraction, etc.) can be calculated to assess the performance characteristics (like mixing efficiency, particle transport, recirculation zones, etc.) of different product designs. This can easily be visualized through plotting options such as contours, streamlines, section slices, particle flows and iso-surfaces to quickly provide useful insights and move forward with design optimization proposals.
Finite Element Method (FEM)
W
e carry out FEM calculations to evaluate the structural
performance of a product and perform complex
analyses on advanced materials like Carbon Fibre
Reinforced Plastics (CFRP), Metal Matrix Composites
(MMC), to understand various complex phenomenon such post-buckling, thermal stress, bonding failure, durability, crack propagation, and more...
A structural analysis allows to:
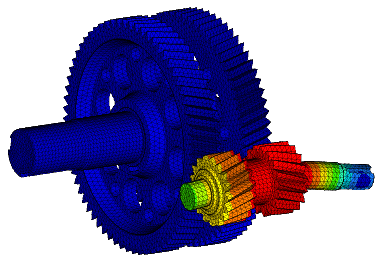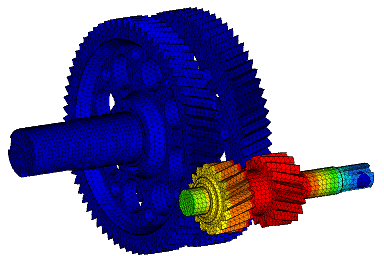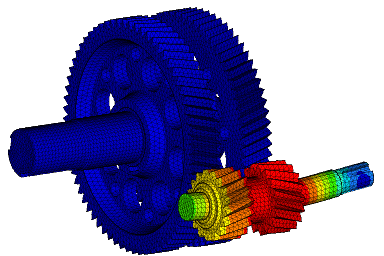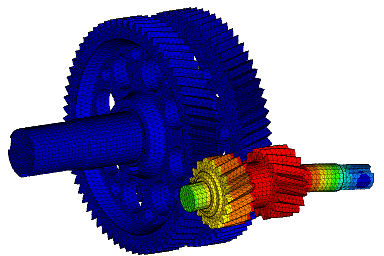
- simulate the behavior of complex physical systems by means of specific calculation codes (pre- and post-processing, thermal analyses, optimizations);
- predict the lifetime for evaluating the reliability of various components using structural simulations;
- understand how a material conducts or insulates heat, how a solid reacts to a thermal load, or how increasing of pressure load causes temperature changes in a solid using thermomechanical simulation;
- foresee resonances and vibroacoustic behavior during operation.
Boundary Element Method (BEM)
I
n engineering, numerical modeling and simulation are widely used for solving complex problems.
The BEM approach is very interesting in this way, as it allows to solve numerous problems, especially those, that require the use of differential equations.
The method is based on the discretization of the solution domain only at the boundaries, reducing the size of the problem and thus simplifying the required input data.
It is based on the resolution of an integral equation defined on the boundary instead of on the direct resolution of partial differential equations as is the case of FEM.
In BEM, the starting equation is reformulated with an integral equation defined on the boundary of the domain (BIE - Boundary Integral Equation), and an integral that correlates the solution on the boundary with the solution in the internal points.
BEM can be widely applied to solve:
- electromagnetic problems associated with electrical machines;
- problems of airborne acoustic emission, fracture mechanics, potential flow around the airfoil;
- problems related to natural frequencies of liquid sloshing in tanks;
- problems related to contact issues, especially in association with the simulation of adhesive contacts.
- all those problems in which it is possible ti define an integral equation.
FEM / BEM – Differences and Advantages
A
dvantages of BEM:
The main advantages of this method can be identified with the simplicity of building a 3D model having to discretize only the surface of the body, the high precision for calculations in which the results on the border have a preponderant importance compared to those inside and with the adaptability to problems with open or mobile boundaries.
Advantages of FEM:
Typical advantages of FEM are found in the simplicity of solving non-linear problems and in the versatility of being extended to transient problems.
Advantages of both, BEM and FEM:
It’s beneficial to verify results by comparing the 2 different methods.
Multi-objective Parametric Optimizations
Advanced optimization algorithms allow us to explore design alternatives by searching a defined design framework to select a combination of design parameters that allows products to be optimized without compromising performance.
We use multi-objective optimization software to identify the best combination of design parameters required to achieve the intended or required product performance and simultaneously adhere to imposed required constraints.
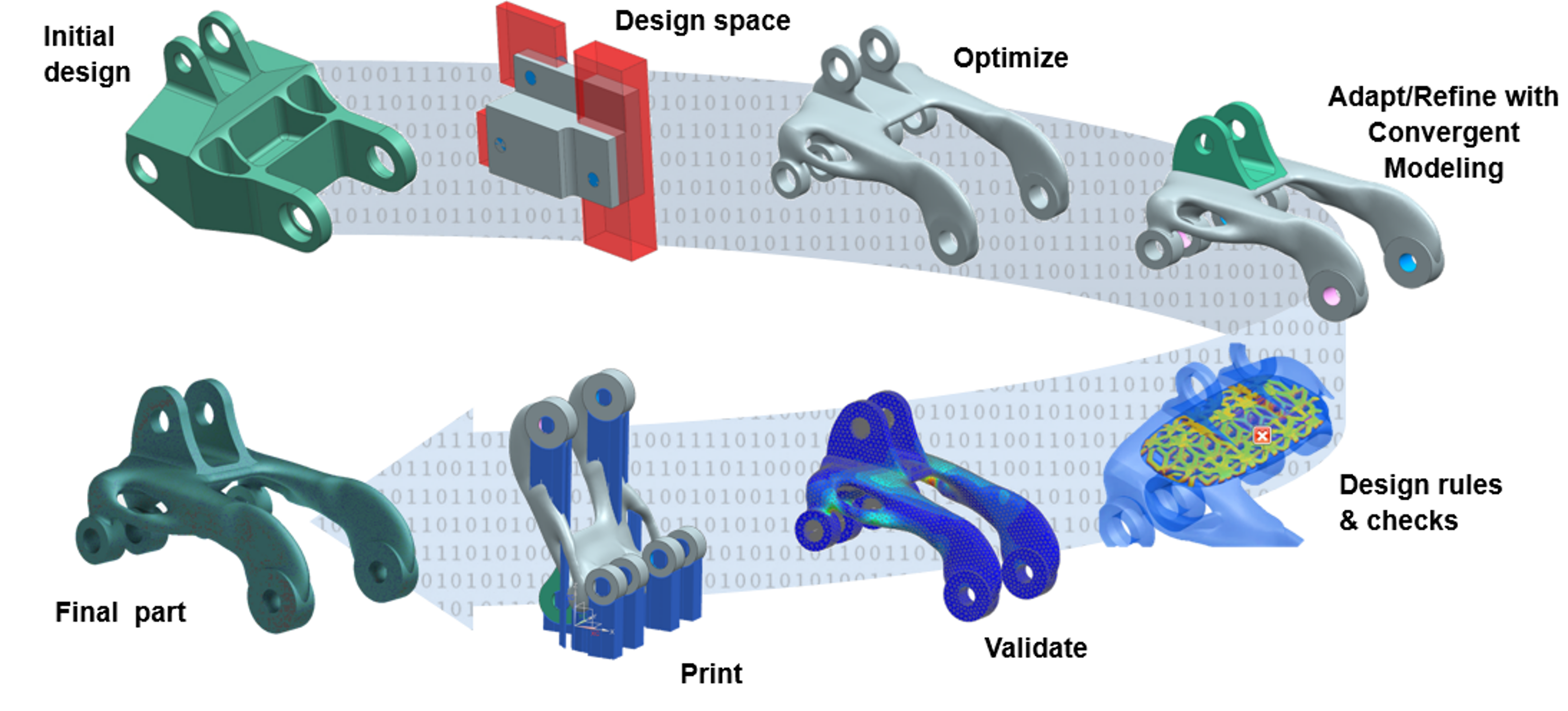
Topological optimization
T
raditional structural simulations allow engineers to verify whether a design will support the required loads.
Through topological optimization, it is possible to improve this process by using loads and constraints as input to generate a new, lighter layout in an already defined volume and define structurally efficient and lightweight concepts in both the design and redesign phases.
Thanks to this mathematical method it is possible to reduce weights, times and production costs in respect of the functional and mechanical requirements.
Copyright © 2022 Dipolo GmbH. All rights reserved.